요약
내부 공변량 변화(internal covariate shift)란, 훈련 중 각 층의 입력분포가 이전층의 매개변수 변화로 인해 발생하는 문제이다.
이 현상은 낮은 학습률과 신중한 매개변수 초기화를 필요로 하여 학습속도를 낮춘다.
이를 해결하기 위해 층의 입력을 정규화(Normalization) 하는 방법을 제안한다.
모델 아키텍처의 일부로 정규화를 포함시키고, 각 mini batch마다 정규화를 수행하는 방법으로,
높은 학습률 사용이 가능하고, 초기화에 대해 덜 신경 쓸 수 있다.
또한 일부 경우에서는 Dropout의 필요성을 없앨 수 있다
최신 이미지 모델에서 적용했을 때, 배치 정규화를 사용하면 14배 더 적은 훈련 step으로 동일한 정확도를 달성하고, 원래의 모델을 큰 차이로 능가한다.
1. 개요
SGD(Stochastic gradient descent)는 딥러닝 훈련에 있어서 효율적인 방법이었으며, 이를 변형한 Momentum과 Adagrad를 통해 SOTA를 달성할 수 있었다.
SGD는 아래 loss를 최소화하는 파라미터 Θ를 찾는다

손실함수 근사를 위해 각 step에서 mini-batch(x1...m)를 사용한 gradient 계산은 다음과 같다

mini batch를 사용했을 때의 장점은 다음과 같다:
- mini batch에서 구한 loss의 기울기(gradient)는 전체 훈련세트(full batch)에 대한 기울기의 근사치로,
배치가 증가함에 따라 이 추정치의 질이 향상된다
- 병렬처리를 사용하면 mini batch를 사용한 연산이 더 효율적이다.
확률적 경사하강법은 단순하고 효과적이지만, hyper parameter에 대한 신중한 튜닝이 필요하다.
훈련은 각 층의 입력이 모든 선행층의 파라미터에 의해 영향을 받기 때문에 복잡해진다.
이로 인해 신경망 내의 파라미터에 대한 작은 변경사항도, 신경망이 깊어질수록 증폭된다.
레이어의 입력분포 변화는 레이어가 새로운 분포에 대해 지속적으로 적응해야 하기 때문에 문제가 발생된다
학습 시스템에 입력되는 분포가 변화하는 현상을 공변량 변화(covariate shift)라고 한다.
이 문제는 주로 도메인 처리(domain adaptaion)으로 처리된다
그러나, 공변량 변화라는 개념은 학습 시스템을 넘어, sub-network나 layer에 적용될 수 있다.
예를 들어, 네트워크가 다음과 같은 수식을 계산한다고 해보자
ℓ = F2(F1(u, Θ1), Θ2)
F1과 F2는 임의의 변환이고, 파라미터 Θ1 과 Θ2 가 loss ℓ 을 최소화 하는 방향으로 학습된다
여기서 Θ2에 대한 학습은 x = F1(u, Θ1)가 하위 네트워크 ℓ = F2(x, Θ2)로 입력되는 것처럼 볼 수 있다

예를 들어, Θ2에 대한 경사하강법 step은 입력이 x인 독립 네트워크 F2와 완벽히 동일하다
따라서, 훈련과 테스트 데이터 간에 동일한 분포를 가지는 것과 같이, 훈련을 더 효율적으로 만드는 입력 분포의 속성은 하위 네트워크 훈련에도 적용된다
이러한 이유로, 시간이 지남에 따라 x의 분포가 고정되어 있는 것이 유리하다
x의 분포가 고정되면, Θ2는 x의 분포의 변화에 따라 재조정될 필요가 없어진다
하위 네트워크에 고정된 분포의 입력은 하위 네트워크 내부의 layer에도 긍정적인 영향을 미치게 된다
Sigmoid 활성화 함수 z = g(Wu + b) [가중치 W와 bias b를 학습, g(x) = 1 / (1 + exp(-x))] 에서,
x의 절댓값이 증가할수록 g'(x)가 0에 가까워진다.
이는 x = (Wu + b) 의 모든 차원이 작은 절댓값을 제외하고 u로 흐르는 기울기가 사라지고 모델의 학습이 느려진다는 것을 의미한다.
그러나, x는 W와 b 그리고 모든 아래 네트워크의 파라미터에 영향을 받으므로, 훈련 중 이러한 파라미터의 변경은 x의 많은 차원을 비선형성의 포화 영역으로 이동시키고 수렴을 느리게 할 가능성이 높다.
이 효과는 네트워크의 깊이가 증가할수록 증폭된다.
포화 문제와 기울기 소실(gradient vanishing)에 대한 문제는 ReLU와 작은 학습률, 신중한 초기화를 사용하여 처리된다.
하지만, 네트워크 훈련 중 비선형성 입력의 분포가 더 안정적 되도록 유지할 수 있다면,
optimizer가 포화 상태에 빠질 가능성이 줄어들고 훈련이 가속화 될 수 있을 것이다.
2. 내부 공변량 변화 줄이기
내부 공변량 변화 : 훈련 중 네트워크 파라미터의 변화로 인한 네트워크 활성화(activation)의 분포가 변하는 현상
훈련 개선을 위해 내부 공변량 변화를 줄이는 방법을 찾아야 한다
입력이 백화(whitening)되면 즉, 평균이 0이고 단위 분산을 가지며 상관관계가 제거된 선형 변환을 거치면 네트워크 훈련이 더 빨리 수렴하는 것이 이미 알려져 있다.
각 layer의 입력을 백화함으로써, 고정된 입력 분포를 만들어 내부 공변량 변화로 인해 발생되는 부정적인 영향을 없앨 수 있을 것이다.
x 벡터를 layer의 입력으로 하고, X를 전체 훈련 세트라고 하자.

정규화 변환은 주어진 훈련 예제 x뿐만 아니라 모든 예제 X에 의존하는 변환이 된다.
여기서 X의 각 샘플은 x가 다른 레이어에 의해 생성되었다면 Θ에 의존한다.
역전파를 위해, 계산되는 야코비안은 다음과 같다

후자의 항을 무시하면 모델 폭발 현상 (파라미터가 무한으로 발산) 의 가능성이 있다.
프레임워크 내에서 layer 입력을 백화하는것은 Cov[x] - 공분산 행렬 계산과 그 역의 제곱근을 계산하는 것을 포함하기 때문에 많은 비용이 든다. 또한 역전파를 위해 해당 변환의 도함수도 생성해야 하므로, 다른 효율적인 방법을 찾아야 했다.
3. Mini-batch를 통한 정규화
각 layer의 입력을 모두 백화시키는것은 비용이 높고, 모든 부분에서 미분가능하지 않기 때문에, 두 가지 간소화 과정을 거친다.
첫 번째는 각 스칼라 feature를 독립적으로 정규화하여 평균을 0, 분산을 1로 만드는 것이다.
d차원 입력 $x = (x^{1}, ..., x^{d})$를 가진 layer에서, 각 차원을 다음과 같이 정규화한다
$$ {x_{b}}^{k} = \frac{x^{k} - E[x^{k}]}{\sqrt{Var[x^{k}]}} $$
위 수식에서 평균과 분산은 전체 학습 데이터에서 사용되는 입력의 각 차원에 대해 계산된 값을 의미한다.
이러한 정규화는 feature가 서로 상관관계가 없더라도 수렴을 가속화한다고 알려져 있다.
다만, 각 입력에 대한 단순한 정규화는 layer가 표현하고자 하는 것을 변경해버릴 수 있다.
예를 들어, Sigmoid에 대한 입력을 정규화하는것은 선형 영역으로 제한하여 활성 함수의 특징인 비선형성을 잃게 된다.
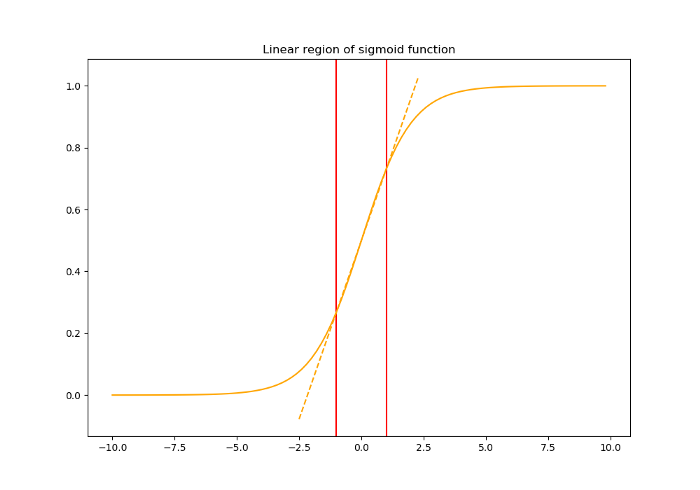
이 문제를 해결하기 위해, 정규화된 값을 스케일링하고 이동시키는 변수 $γ^{(k)} , β^{(k)}$ 를 도입한다.
$$ y^{(k)} = \gamma ^{(k)} \hat{x}^{(k)} + \beta ^{(k)} $$
이 파라미터는 모델과 함께 훈련되며, 네트워크의 표현력을 복원시킨다.
실제로 $ \gamma ^{(k)} = \sqrt{Var[x^{k}] $ 이고 $ \beta ^{(k)} = E[x^{k}] $ 으로 값을 설정하면, 최적의 경우 원래의 활성화를 복구할 수 있다.
전체 훈련 세트를 기반으로 하는 배치 설정에서는 전체 세트를 사용하여 활성화를 정규화할 수 있지만, 이 방식은 확률적 최적화를 사용할 때는 비현실적이다. 따라서 두번째 간소화를 도입한다.
SGD에서 mini batch를 사용하기 때문에, 각 mini batch는 각각의 활성화 함수에 대한 평균과 분산의 근사치를 계산한다.
이를 통해 얻은 통계량은 gradient 역전파에 완벽하게 관여할 수 있게 된다.
size가 m인 mini-batch B의 배치 정규화 변환(Batch Normalizing Transform) 알고리즘은 다음과 같다.

mini-batch에 의존하는 activation의 정규화는 효율적인 훈련을 가능하게 하지만,
추론 중에는 어떤 입력이 들어올지 알수 없으므로 batch에 대한 평균과 분산을 구할 수 없다.
따라서 추론 과정에서는 학습을 진행하는 동안 계산한 값으로 고정시킨다.
배치 정규화의 장점은 다음과 같다
- 어떠한 활성화 네트워크에도 사용 가능
- 네트워크의 학습 속도 증가
- 높은 학습률을 사용해도 기울기 폭발/소실, local minima에서의 고착과 같은 문제 해결 가능
- 특정 값에 대한 결정적 값을 생성하지 않음 -> 네트워크의 일반화가 좋아짐
'AI' 카테고리의 다른 글
| 모개숲 딥러닝 스터디 - 5. Segmentation Anything (0) | 2024.04.04 |
|---|---|
| 모개숲 딥러닝 스터디 - 4. Nightshade (0) | 2024.03.29 |
| 모개숲 딥러닝 스터디 - 3. ResNet : Deep Residual Learning for Image Recognition (1) | 2024.03.24 |
| 모개숲 딥러닝 스터디 - 2. You Only Look Once Unified, Real-Time Object Detection (1) | 2024.03.17 |
| 논문 리뷰 - The Era of 1-bit LLMs:All Large Language Models are in 1.58 Bits (0) | 2024.03.14 |
