Introduction
최근 파라미터 없이 학습률을 자동 조정하는 적응형 학습률 (Adaptive Learning Rate) 방법들이 주목받고 있음.
Prodigy는 이 중 가장 유망한 접근법인 D-Adaptation 방법을 개선한 것.
D-Adaptation은 볼록 목적함수(convex objective function) $f$가 주어졌을 때,
해집합 모든 $x^*$에 대해, 초기해 까지의 거리 $D = \|x_0 - x^*\|$에 대한 하한을 유지하는 방식이다.
$\min_{x \in \mathbb{R}^p} f(x)$
이 방법은 진짜 D에 가까운 값으로 수렴한다. D는 비연속(non-smooth) 최적화 방법에서 학습률을 설정하는데 쓰인다.
$$\gamma_{k+1} = \frac{D}{\sqrt{\sum_{i=0}^{k} \|g_i\|^2}}$$
분모는 AdaGrad의 학습률 수식에 기반하였음.
이 방법은 Adam에서의 학습률를 추정하는데 쓰일 수 있으며, 다양한 문제에서 SOTA를 달성함
D-Adaptation은 실제 D를 사용하여 학습률을 지정하는 것 만큼 빠르게 수렴하는것을 보여줌
그러나 비수렴(non-asymptotic) 수렴 이론상의 최악의 경우가 존재, 이를 보완한 Prodigy를 제시함
Prodigy Approach
D-Adaptated Dual Averaging에서, 반복 k에서의 기울기는 가중치 $λ_k$로 스케일되는데, 이는 오류 항을 초래함:
$D\text{-adaptation error} = \sum_{k=0}^{n} \lambda_k^2 \gamma_k \|g_k\|^2$
이 이론은 $λ_k$중 가장 큰 $λ_n$을 사용하여 상한으로 설정하기때문에 위와 같은 오차가 발생.
따라서 $λ_{k}^{2}$를 $λ_{n}^{2}$으로 대체하는것은 $\frac{D^2}{d_0^2}$ 만큼의 배율 오류항이 발생하게 된다
이를 해결하기 위해 AdaGrad와 유사한 방법을 사용하여 오류항을 처리한다.
기존 AdaGrad에서는 기울기의 제곱 합을 학습률의 분모로 사용하지만,
Prodigy에서는 각 기울기에 대응하는 거리 추정치 $d_i$의 제곱을 추가하여 기울기의 제곱과 곱한 값으로 분모를 구성한다.
이러한 방식으로, Prodigy는 Gradient Descent와 Dual Averaging algorithm 모두에서 오류항을 제어할 수 있고,
$d_k$값의 비감소적 특성으로 인해 학습률을 증가시킬 수 있어 학습과정에서 빠른 수렴을 가능하게 한다.

1: 입력값 설정
$d_0$ : 목적함수로 부터 $x_0$까지의 초기 거리추정치
$x_0$ : 최적화를 시작할 파라미터의 위치
$G$ : 기울기의 추정된 최대 norm
3: 기울기 계산
$g_k$는 f의 $x_k$에서의 기울기
4: 가중치 $λ_k$ 선택
5: 학습률 계산
$n_k$는 $\eta_k = \frac{d_k^2 \lambda_k}{\sqrt{G^2 + \sum_{i=0}^{k} d_i^2 \lambda_i^2 \|g_i\|^2}}$의 합으로 계산됨.
Experiments
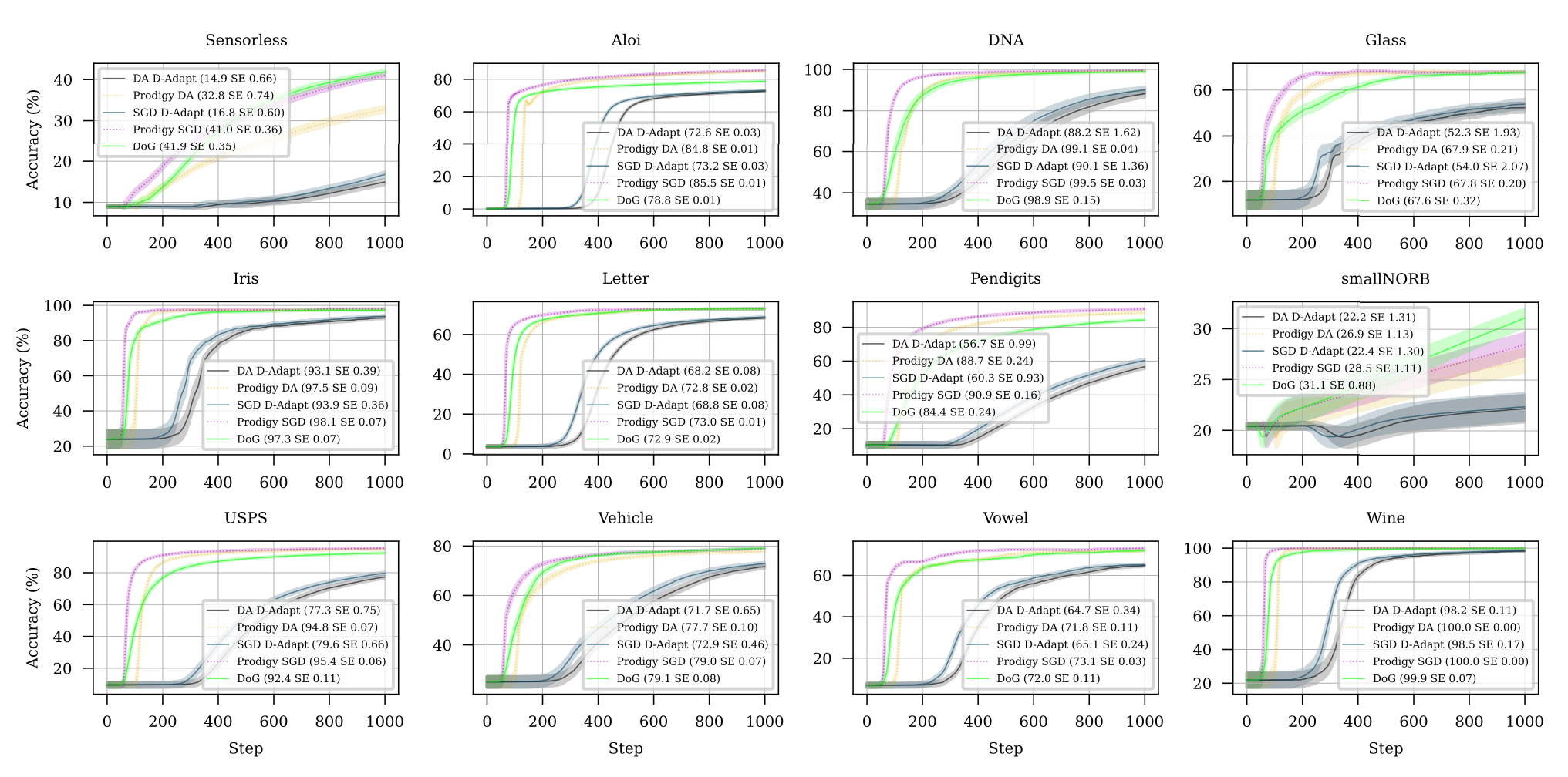

다양한 데이터셋을 가지고 비교한 결과.
다른 optimizer들과 비교하여 적은 epoch로 낮은 Train Loss를 달성하는 것을 볼 수 있다
또한 Test 정확도 측면에서도 타 알고리즘보다 우위를 보여준다
