논문 리뷰 - DenseFormer: Enhancing Information Flow inTransformers via Depth Weighted Averaging

META_BS 2024. 4. 8. 18:32

0. Abstract

Transformer 모델구조가 NLP부터 음성인식, 이미지 인식까지 매우 범용적으로 쓰임.

기본 Transformer에 약간의 파라미터 증가로 모델 복잡성(Perplexity)를 개선하는 DenseFormer를 소개한다

Depth-Weighted-Average(DWA): 각 Transformer block 뒤에 현재와 과거의 가중평균을 반영하는 연산

DenseFormer는 데이터면에서 효율적이고, 더 깊은 Transformer model과 동등한 성능을 보인다.

또한 기본 Transformer보다 메모리 효율적이고 추론시간도 짧다.

1. Introduction

Transformer 아키텍처가 현대 NLP의 중심을 맡고 있다. Transformer 구조는 SOTA달성에 큰 역할을 했으며, 파라미터 수를 크게 증가시킴으로써 가능했다.

그러나, 거대모델은 높은 연산량과 많은 메모리를 필요로 한다.

이를 해결해보고자 작은 모델로 많은 step을 반복하려는 시도가 있었으나, 더 많은 학습은 더 큰 데이터셋을 필요로 하기 때문에 어려움이 있었다.

더 나아가, 모델의 깊이가 깊어질수록 성능향상 폭이 낮아진다는 사실이 최근에 발견 되었다.

이러한 문제를 해결하기 위해 다양한 해결법이 제안되었는데,

DenseNet(Huang et al. 2017)은 layer들이 이전 layer들을 직접적으로 접근할 수 있도록 만들어 이 문제를 완화시켰다.

DenseNet과 비슷한 직관을 사용하여 Transformer에 적용시킨 구조가 DenseFormer이다.

더 깊은 Transformer모델보다 같은 성능을 보이지만, 작은 사이즈, 빠른 속도, 적은 추론 메모리 사용 등 이점이 있다.

중요한것은 학습 데이터를 늘리지 않고도 위의 성능향상을 달성했다는 것이다.

2. Related work

더 크고 깊은 모델을 사용하는 것이 뛰어난 성능을 제공한다고 알려저 있음(Pette et al. 2023b)

그러나 모델의 깊이를 늘릴수록 얻는 이득이 점점 감소

예전 CNN에서 동일한 문제가 발생했고, 이를 해결하기 위한 방안이 등장했었다(ResNet)

더 나아가 DenseNet은 모든 이전 layer의 출력에 접근함으로써 더 큰 이득을 보았다

비슷한 직관을 바탕으로, 모든 block이 모든 이전 block의 출력에 직접 접근할 수 있게 하는 DenseFormer를 제안한다

Depthwise Attention과 같은 다양한 논문에서 이전 layer를 참조하는 방법의 장점은 이미 여러번 탐구된 바 있다.

그러나 Depthwise Attention은 행렬 곱 연산(dot product)를 수행하여 높은 오버헤드가 발생했다.

Transformer는 처음 설계된 이후로 다양한 작업에 사용되고 있으며, LLM은 큰 학습비용때문에 아키텍처의 선택은 대체로 보수적이다.

여기에는 Activation function 변경, LayerNorm 대신 RMSNorm의 적용, FeedForward와 어텐션의 병렬연산 등 작은 변화가 포함된다.

DenseFormer는 이런 기존의 제안들과 함께 사용될 수 있으며, block간 작동하는 DWA모듈만 추가하기 때문에 기존의 Transformer block 내부구조에 영향을 미치지 않는다.

3. Method

Figure 1. DenseFormer의 구조

a) 첫번째 블록은 DWA의 가중치 $[a_{0,0}, a_{0,1}]$을 사용하여 과거와 현재의 중간표현 ${X_0, X_1}$의 평균을 계산한다.

b) DWA의 가중치 행렬. 깊이 i 에서 i+1개의 가중치를 가진다. Dilation(확장)의 증가는 행렬을 희소하게 만들어, 모델의 복잡도 감소 없이 계산 오버헤드를 감소시킨다.

Transformer 구조는 아래와 같다:

$X_0 := \text{Embedding}(X)$
$\forall i = 1, \ldots d, X_i:= B_i(X_{i-1})$
$\text{Transformer}(X) := X_d.$

기존 Transformer의 구조에서 바뀐점은 각 transformer 블록 뒤에 Depth Weighted Average module(DWA)를 추가한 것 뿐이다.

깊이 i 에서의 DWA 모듈은 아래 세가지의 가중평균을 계산한다.

1. 현재 블록인 $B_i$ 에서의 출력

2. 모든 이전블록 $B_{j<i}$ 에서의 출력

3. 임베딩된 입력 $X_0$

깊이 i 에서의 DWA 모듈의 가중치 행렬은 $a_{i,0} , ... , a_{i,i}$ 로 표현될 수 있으며, Fig 1에 시각화되어있다.

기존의 Transformer 모델에서 추가된 파라미터는 a 행렬이 전부이다.

DenseFormer는 아래와 같이 요약될 수 있다:

$X_0 := \text{Embedding}(X)$
$Y_0 := X_0$
$\forall i = 1, \ldots d, X_i := B_i(Y_{i-1})$
$\forall i = 1, \ldots d, Y_i := \text{DWA}_i(\{X_0, \ldots , X_i\}) = \sum_{j=0}^{i} \alpha_{i,j} \cdot X_j$
$\text{DenseFormer}(X) := Y_d$

DenseFormer 구조의 영향은 아래와 같다.

- 모델 크기로 인한 오버헤드가 거의 없음 :

깊이 i 에서의 DWA 모듈은 i + 1개의 가중치를 가지고 있다.

따라서 깊이 d 에서, 추가적인 파라미터의 개수는 $d(d+3) / 2$ 개가 된다. 통상적인 모델 깊이(100블록보다 적은)를 고려해보면, $10^{3}$개 정도의 파라미터를 가지게 되는데, 이는 모델 전체를 고려했을 때 무시가능한 정도의 크기이다.

- 메모리 오버헤드가 거의 없음:

DWA가 블록의 출력과 임베딩된 입력 X에 접근해야 하지만, 이러한 값들은 표준 Transformer 구조를 사용했을 때도 동일하게 저장된다. 훈련중에는 블록의 출력이 역전파를 위해 메모리에 저장되고, 추론시에는 KV 캐시에 저장된다.

따라서 DenseFormerd의 메모리 오버헤드는 무시할 수 있을 정도이다.

- 연산 오버헤드

DWA 모듈 출력의 계산은 (배치 사이즈 x 시퀀스 길이 x 은닉 차원)에 대한 평균을 요구하기 때문에 계산 비용이 증가한다.

DWA의 효율적인 구현을 제공하기 위해, DenseFormer변형을 구축할 수 있는 두 가지 하이퍼파라미터, DWA dilation(확장)과 DWA periodicity(주기성)를 소개한다.

dilation 인자 k와, periodicity p를 가진 DenseFormer를 $k x p - DenseFormer$ 라 한다.

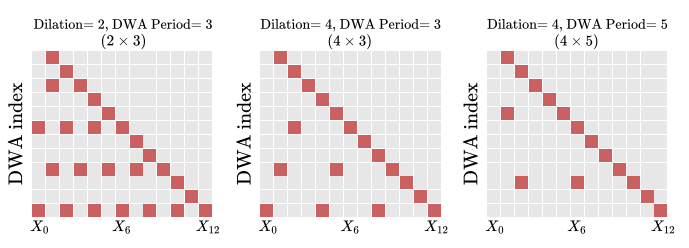
Figure 2. dilation과 period를 적용한 DWA 가중치 행렬

Fig 1b와 비교했을때, 일부 행에만 일부 가중치가 있는것을 확인할 수 있다.

dilation과 period를 증가시키면 a 행렬이 더욱 희소해지며, 모델의 복잡성(perplexity)을 유지하면서 연산량을 감소시킨다.

3.2 Dilated DenseFormer

연산 오버헤드를 줄이기 위해, DWA 가중치를 주기적으로 0으로 설정하여 행렬을 희소하게 만드는 dilation 매개변수를 도입한다.

각 DWA모듈은 k번째 블록의 출력을 받으며, 여기서 k는 dilation 인자가 된다.

깊이 i에서 DWA 모듈에 대해, k의 dilation 인자는 ${{X_j | j<=i, j=i(modk)}}$에 대한 가중평균만을 계산한다.

dilation 인자를 적용시킨 구조는 아래와 같이 표현될 수 있다:

$X_0 := \text{Embedding}(X)$
$Y_0 := X_0$
$\forall i = 1, \ldots, d, X_i := B_i(Y_{i-1})$
$\forall i = 1, \ldots, d, Y_i := \text{DWAdilated}_i(\{X_j | j \leq i, j \equiv i \mod k\})$
$\text{DenseFormer}(X) := Y_d$

3.3 Periodic DenseFormer

DWA 가중치를 희소화하기 위한 dilation의 대안적 방법으로, DWA 모듈의 가중치를 더 드물게 아키텍처에 추가하는 방법이 있다.

모든 블록 이후가 아닌, p개의 블록마다 DWA를 추가. 여기서 p는 DWA per라고 한다

dilation k와 period p를 가진 DenseFormer를 $ k x p - DenseFormer $라고 하며, 아래와 같이 요약된다 :

$X_0 := \text{Embedding}(X)$
$Y_0 := X_0$
$\forall i = 1, \ldots, d, X_i := B_i(Y_{i-1})$
$\forall i = 1, \ldots, d, Y_i := \begin{cases} \text{DWAdilated}_i(\{X_j | j \leq i, j \equiv i \mod k\}) & \text{if } p \mid i \\ X_i & \text{if } p \nmid i \end{cases}$
$\text{DenseFormer}(X) := Y_d.$

p를 증가시킴으로써, DenseFormer의 계산 비용을 더욱 줄일 수 있다. 눈에띄는 성능 저하 없이 속도를 향상시킬 수 있다.

$ k x p - DenseFormer $ 는 일반 DenseFormer에 비해 1/kp의 연산 오버헤드를 지닌다.